The numbers via which we express quantities can be expressed as time, weight, distance, and so on. For instance, studying calculus, which is used to investigate rates of change as well as optimization issues, requires a solid understanding of quantity. The use of quantity in practical applications is another crucial component of quantity in mathematics. For instance, position, velocity, or acceleration are used in physics to describe the motion of things and to anticipate how they will behave. The analysis of quantity in math is important because it creates the basis for a profound comprehension of mathematical principles and procedures, in addition to enabling one to execute operations on quantities.
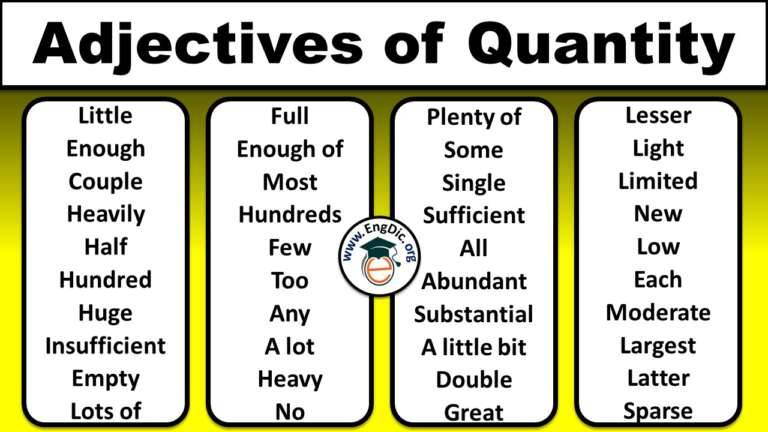
(a) few or (a) little – expressions of quantity
A quantum is a plurality if it is numerable, a magnitude if it is measurable. Of these, limited plurality is number, limited length is a line, breadth a surface, depth a solid. Vector quantities are quantities with both magnitude and direction. Let’s see a few examples of quantity in daily life. One important point to be remembered is that we cannot compare quantities that have different dimensions. For example, a square of side length of 2 inches will have an area of 4 inch2.
Quantifiers Examples
Quantity or amount is a property that can exist as a multitude or magnitude, which illustrate discontinuity and continuity. Quantities can be compared in terms of “more”, “less”, or “equal”, or by assigning a numerical value multiple of a unit of measurement. Mass, time, distance, heat, and angle are among the familiar examples of quantitative properties. For instance, alcohol by volume (ABV) represents a volumetric ratio; its value remains independent of the specific units of volume used, such as in milliliters per milliliter (mL/mL).
Mathematical Quantity
This page will help you understand what quantity is. Also, you will get to know real-life examples of quantity. Mathematical models are used in many disciplines, including engineering, finance, as well as the natural sciences, to describe and analyze phenomena that occur in the actual world. Success in these professions depends on one’s capacity to manipulate numerical data and make predictions using mathematical models.
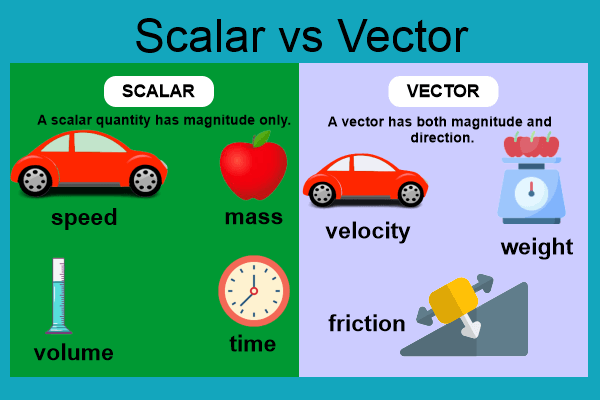
Quantity is a tool used in mathematics for problem-solving, developing mathematical models, and making predictions about the relationships between various quantities. Scalar quantities are the quantities of physical space and time that only have one dimension, magnitude. A magnitude or even a numerical value is sufficient to provide a complete description of it. The scalar amount does not include directions. Quantities can also be interpreted in the form of numbers; for instance, this book has 55 pages, or the container has an ‘x’ quantity or the number of black pens. Quantities can indeed be expressed numerically as distance, time, mass, etc.
Well, on adding the numbers 3560 and 1200, we get 4760. Here, assume that you find a container filled with 4760 glasses of companies A and B at Sky shop, so here, 4760 glasses are the quantity of glasses A and B in a container. The next day, she went back to the village and showed the proof of the false weight he made yesterday. So, he came to know that it was 16 packets of sugar and apologised for not repeating the mischief again. Let’s say she bought 20 packs of sugar and discovered something was off.
- A fundamental idea in mathematics called quantity is essential to many fields of study as well as practical applications.
- The two types of quantities are scalar and vector.
- This is so because the units are unchanging and the qualities and relations we are studying and expressing in mathematics are abstract.
- The use of quantity in practical applications is another crucial component of quantity in mathematics.
Establishing quantitative structure and relationships between different quantities is the cornerstone of modern science, especially but not restricted to physical sciences. Physics is fundamentally a quantitative science; chemistry, biology and others are increasingly so. Setting the units of measurement, physics covers such fundamental quantities as space (length, breadth, and depth) and time, mass and force, temperature, energy, and quanta. Magnitude (how much) and multitude (how many), the two principal types of quantities, are further divided as mathematical and physical. In formal terms, quantities—their ratios, proportions, order and formal relationships of equality and inequality—are studied by mathematics.
The length of the sides of a square also has a quantity, or magnitude, from which we can find even more quantities. For example, the square shown below has a side length of 3 centimeters. Spanish adverbs are words used to modify verbs, adjectives and other adverbs, as well as whole sentences. They provide information concerning time, place, manner, or quantity, among other aspects. Quantities can also be understood as numbers; for example, this book has 55 pages or the container has ‘x’ quantity or the number of black pens.
The mathematical usage of a quantity can then be varied and so is situationally dependent. Quantities can be used as being infinitesimal, arguments of a function, variables in an expression (independent or freelance taxes dependent), or probabilistic as in random and stochastic quantities. In mathematics, magnitudes and multitudes are also not only two distinct kinds of quantity but furthermore relatable to each other.

